

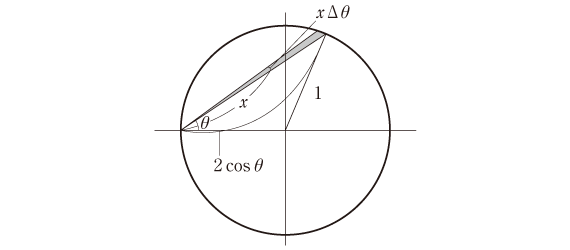
まずθ、Δθを固定して、θは0からΠ/2まで変わるので、
さて、円内の2つの点のうち、原点からより遠いほうをA、近いほうを
Bとよびます。
(線分の長さはB―A で1回の計算で、重ねて計算する必要はありません)
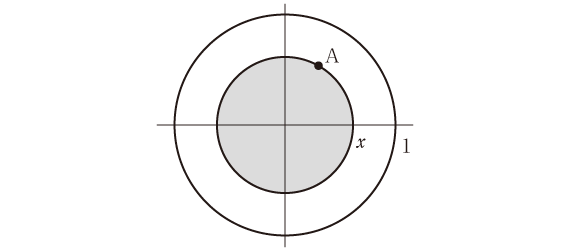
Aが半径xの円上を動くとき、その円内(上図の網掛け部内)にある
BとAとの距離の期待値は、
したがって答えは、
1 2 1 2∫ 2πx・πx ・ 32x/9π dx ÷ ∫ 2πx・πx dx 0 0
=128/45π
この式の意味は、解かり難いのかも知れませんねぇ~ ![]()
![]()
補足説明ですが、この積分中の2πxは、Aが動く半径xの円のドット数の
ようなものであり、πx2は、Bが動く円内のドット数のようなものであり、
それらをかけ合わせると、線分AB の総本数のようなものになります。
以上でーす! ![]()
![]()
![]()
![]()
![]()
問題の解けた方は、かなりの「数学好き」ですよねぇ~ ![]()
![]()

アハハハ!!
実は、設計図面を書く為のCADと言われるソフトが世の中には沢山
ありますが・・・ ![]()
3DCADと言われる「3次元のCADが抱える」点群処理の問題を
解決する為の有効なソフトは完成していません。 ![]()
![]()

現在の解決策としては、点とベクトルを利用した新たなCADの開発
を行えば、問題はある程度解決しますが・・・ ![]()
それ以上に「画期的な新開発」とは・・・ ![]()
![]()
![]()

この問題から得られる内容を利用して「3D CADの点群問題」に
取り組めば・・・ ![]()
「問題の解決が図れる可能性は極めて高い」と言う事をMYブログに
書いておきます。 ![]()

もう20年以上も前の事ですが、私もこの問題に向き合って、特許権
を取得した事があるので、言える事ですが・・・ ![]()
![]()
このブログに書いた内容は確実に「特許も取れる」と思います。![]()

私は、もう若くは無いので開発は行いませんが、興味のある専門家の
一助になれば、幸いでぇーす! ![]()
![]()

IOTとの連携したCADの開発も画期的で、面白いと思いますよ!
AI技術を絡めると、更に・・・ ![]()
![]()
頑張れ! 心のある若き企業の戦士達! ![]()
![]()
応援しているぞぉ~ ![]()
![]()
彼女も、こんなに応援してくれてるよぉ~ ![]()
![]()

アハハハ!!!




