このブログを読むには「専門知識が必要」です。
従いまして、先ずは「専門知識のある方」の為に、ブログを書いて置きます。
専門知識の無い方は、スルーしてください。
専門知識の無い方でも、このブログを読まないで、内容の理解が出来る様に、
簡単に略した「第二弾のブログ」も、引き続き書く事に「挑戦」を致します。
アハハハ
生物の個体数、新製品の販売数、プログラムのバグ発見数など、当初は少なく、中途で大きくなり、その後また少なくなるような現象は多くあります。それを
時間の推移と累積量をグラフにすると、下図のようになります。これを成長曲線といいます。
代表的な成長曲線に、ゴンペルツ曲線とロジスティック曲線があります。
両者とも、似たようなS字型の曲線で、時間xが経つにつれ、増加が止まり一定値Kに近づきます。ロジスティック曲線は変曲点を中心に左右対称になりますが、ゴンペルツ曲線は対称性がないのが大きな特徴です。
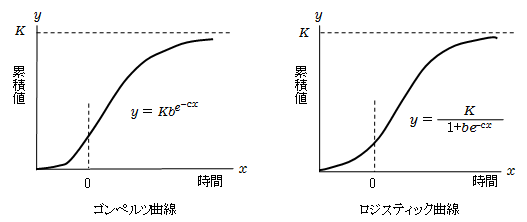
実際には、時間が負になるのは不適切ですが、t=x+t0のような変換により、t≧0としてこれらの曲線を利用します。
ゴンペルツ曲線(Gompertz curve)ゴンペルツ曲線は、 ・・・ゴンペルツ曲線の式
・・・ゴンペルツ曲線の式
をグラフにしたものです。
この式は、
dy/dx = Ay×e-Bx ・・・微分方程式
から得られたものです。
dy/dx は、yの増加率を示しています。すなわち、yの増加率は、
直前のyに比例して増加する要因
時間xに伴い指数的に減少する要因
に関係することを表しています。

ゴンペルツ曲線は、このような性質をもった曲線です。
右図は、K=1として、bとcを変化させたものです。
x→∞ のとき:e-cx→0、b0=1、y→K
x=0 のとき:e-cx=1、y=Kb
x→-∞のとき:e-cx→∞、y→b∞→0
(0<b<1 であることが必要です)になります。
b=0.3、c=0.5のとき(赤線)のグラフでいえば、x0(x=0)のとき、y0=Kb=1×0.3=0.3になっています。bはy0の値を決める要素であり、cは傾きの程度を示していることがわかります。
なお、yがαKになるxは、 = αK
= αK
より、次の式が得られます。
x=(1/c)*log(logb/logα)
ここで、b=0.3、c=0.5のときに、いくつかのαを与えると、次のようになります。
x=(1/0.5)*log(-1.204/logα)
α= 0.5 0.5 0.9 0.99
x= 1.104 4.872 6.312 9.572
この曲線が、プログラムバグ発見数の累積だとすれば、95%のバグが発見されるのはx=6.3の時点であると予想されます。
以上が、成長曲線の代表であるゴンペルツ曲線です。 ![]()
近年は、変曲点を中心に左右対称になるロジステック曲線が、金融工学の専門家には「注目」されていると思われますが、変曲点には対称性がない大きな特徴を
持つゴンペルツ曲線を成長曲線を用いて「投資先の選別」には「利用したい」と考えています。 ![]()
![]()
![]()
![]()
アハハハ!



今年の相場に向かう為の「仕事始め」は、投資銘柄の選別から始めます。
「投資銘柄の新たな選別」に関して、ブログには「成長曲線」の詳細に
ついて書いて置きます。 ![]()
アハハハ!!

