マーケットリスク・パラメータ表について

[NGTNさん]

     

はい、固い話です。バリカタです。数学苦手な人は頭痛くなりますよ。私もいっぱいいっぱいです。

マーケットリスク・パラメータ表のα版がリリースされて、ファイルを開いてみたはいいけど、ヒストリカル・ボラティリティってなあに？　3σってなあに？と思った人が多いと思います。みんかぶさんとしては、あとから徐々に使い方を説明していくつもりかもしれませんが、現状の情報ではとっつきにくくアイデアや質問も出しづらいと思われるので、背景知識を説明したいと思います。（私は、金融工学や数理ファイナンスを学んだわけではないので怪しいところもあるかもしれません。変だと思ったら自分で調べて下さいね。）


まずは、金融の世界でのリスクとリターンの意味について。リスクというのは結果がどれくらいばらくつかという不確実性のことです。損失を出す可能性もリスクですし、利益を出す可能性もリスクです。リターンについては、既に実現したリターンと未来に予想される期待リターンがあります。当然リターンについても、結果が損失であろうと利益であろうとリターンと言います。リスクは「標準偏差」、期待リターンは「期待値」と表されることが多いです。

例を挙げると、サイコロを振って、偶数が出たら1000万円貰えて、奇数が出たら1000万円払うというゲームを考えた場合、何回も繰り返すことが出来るのなら、これはハイリスク・ノーリターンになります。ハイリスクだからといってかならずしもハイリターンにはならないのです。投資商品も同様で、EB債のようにハイリスク・ローリターン（下手するとマイナスリターン）の商品もあります。


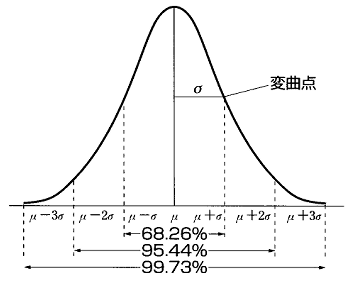
投資の世界では、横軸にリターン、縦軸に確率を取って、その確率分布は正規分布曲線とすることが多いです。ファットテールの問題などもありますが、以降はこの正規分布曲線を前提に話を進めていきます。添付画像1が正規分布曲線で、中央の一番確率の高いところが平均リターンになり、平均に近いほどその結果になる確率は高く、平均から両端へ離れて行くほど確率は低くなります。この曲線が横へなだらかに広がる場合は、平均から離れた位置での事象の発生確率が高い、つまり結果がばらつく（=リスクが高い）ということになります。

えーと、ここまでこの説明でわかりますかね？ googleで「正規分布」や「標準偏差」で検索していただくともっとわかりやすく説明しているところが出てくるかもしれません。

話を続けます。標準偏差は画像2の計算式で計算されます。言葉で書くと、「個々の値と平均との差の二乗の和をデータ数で割って、それの平方根を求めたもの」が標準偏差になります。一般的に、σ（シグマ）で表され、この値が大きいほど、結果がばらついていることになります。

正規分布においては、平均値からの±σの幅のなかに、全体の事象のうちの68.26%がおさまります。例えば、平均リターンが100、標準偏差が5だった場合、68.26%の事象が95～105の間におさまるということです。同様に、±2σの幅の中には95.44%の事象がおさまり、先ほどの数字を使うと、90～110の間に95.44%が入るということになります。

ここでようやく、マーケットリスク・パラメータ表（α版）に出てくる、3σという数字の説明になります。一般的に考えれば、前出の標準偏差σの3倍の数字ということになります。コミュの方に、いくつか細かい不明点を質問しているのですが、
http://minkabu.jp/community/show/4409
多分、計算方法はこうやっているのだろう、というのを書きます。

まずは、60営業日データだったら、対象銘柄の過去60日の終値を読み込みます。その日の終値からその前日の終値を引いたものを日次リターンとし、これを60日分繰り返して、日々のリターンを出します。そしてそのリターンの平均と個々のリターンの差を計算し、これの二乗の総和をデータ数で割って、その平方根を計算したものが標準偏差σになります。ここまでの計算で出したσは、1営業日後の結果のばらつき度合いを示すものになり、株価だったら単位は円になります。

マーケットリスク・パラメータ表での3σは数字が大きいので、おそらく年率換算をしていると思います。日数が経過していく場合、統計学では日数の平方根に比例してリスクが増加していくので、一般的には営業日を250日として、√250をσに掛けて、一年という単位でのリターンのばらつきを表しているのだと思われます。

標準偏差σというのは、あくまで過去のデータから出されたものであって、未来の動きを保証するものではなく、その銘柄や通貨の過去の値動きがどれくらいなのかを数字として把握し、資産変動リスクを管理するのに役立てるものだと思います。あと、最大損失額を想定する、VaR（Value at Risk）という概念も知っておくと良いかもしれません。

頭が痛くなってきたかもしれませんが、次のヒストリカル・ボラティリティにいきます。計算式は画像3になります。終値を前日終値で割ってその常用対数をリターンとして使い、標準偏差を計算するようです。何故ヒストリカル・ボラティリティで対数を使うのかと言うと、例えば1000円の株価が500円になって、また1000円になった場合、変動幅は同じでも変動率が-50%、+100%と大きく変わってきてしまうためです。ヒストリカル・ボラティリティでは変動率を使うので、この変動率を等価にするために対数を用います。

マーケットリスク・パラメータ表のヒストリカル・ボラティリティ（H-Vol）の計算方法はおそらく、営業日分の終値を読み込み、終値を前日終値で割ってその常用対数を求めて、常用対数計算後の個々のデータから平均を引き、その差の二乗の和を常用対数計算後のデータの数で割って、平方根を求めて、年率換算の√250を掛けたものだと思われます。標準偏差なので、含まれる確率は68.26%ですね。


色々と小難しいことを書いてきましたが、「リスクというのは結果のばらつきのこと」「リスクは標準偏差σで表され、σが大きいと資産変動も大きくなる」くらいの理解で良いと思います。

機関投資家は、標準偏差や資産クラス間の相関関数などからポートフォリオ全体のリスクを計算しているのでしょうけど、そこまでやることが個人投資家にとって必要かというと微妙なところです。

とりあえず現状では、「マーケットリスク・パラメータ表」が示す数字を理解することと、それを実際にどう投資行動に生かしていくかの間には大きな落差があるので、それをどうやって埋めて実際に使えるものにしていくかですね。

私なんかは（為替やったことないですけど）、各為替間の動きの相関関数と、合成ポジションを組んだときのスワップ金利の表示などもしてもらえると、資産全体での変動を抑えつつスワップ金利を受け取るポジションを組むのに使えるかなーと思ったりするのですが、こんなことを必要とする人は少数かもしれませんし、「いかに多くの人が気軽に利用できるものにしていくか」の方向で発展させていくのが重要だと思います。

[パプリカさん]

NTGNさん
大変分かりやすく、参考になりました。今後の「みんかぶラボ」の展開に期待しましょう。

パ

[笑福来 三枝 さん]

NGTN先生　おはようございます。
堅いお話は絶好調ですね、流石です。

＞みんかぶさんとしては、あとから徐々に使い方を説明していくつもりかもしれませんが、現状の情報ではとっつきにくくアイデアや質問も出しづらいと思われる

肝心なのは書かれていました通り、背景ですね。
先生の話を読むにも下地がないとなんとなく解った気に
なるだけです。みんかぶさんにはもっと目線を下げて
下地を説明していただけると助かります。
そんなの知ってて当たり前と思っていただくと、交流になりませんから。

NTGN先生　はっきりと言っていただいてありがとうございます。

[まめとぷーこさん]

とても、勉強になります。
ありがとうございました。
NGTN先生、また遊びにきます！

[NGTNさん]

パプリカさん、
こんにちは。分かりやすい、と言って頂けるとありがたいです。今後の発展に期待ですね。

笑福来　三枝　　さん、
こんにちは。調子に乗って書きまくってしまいました。みんかぶさんは、とりあえずα版を出して、フィードバックを得ようと思ったのでしょうね。リリースしてみたはいいけれど、大多数の方にとっては、標準偏差や正規分布の概念は馴染みが無く、彼我の間に距離を感じる結果になったのだと思います。
まだまだα版ですから、今後の発展に期待しましょう。

まめとぷーこさん、
いえいえ、どういたしまして。また遊びに来てくださいね。